Chapter 1 Martingales

Probability Setup

A probability space is given by $(\Omega, \mathcal{F}, \mathbb{P})$.

Definition: Conditional Expectation

$X \in m\mathcal{F}, \mathbb{E}[\lvert X\rvert] < \infty, \mathcal{G} \subset \mathcal{F}$. The conditional expectation $\mathbb{E}[X \mid G]$ is a random variable $Y$ such that:

$Y\in m\mathcal{G}$.
For all $A \in G$,
\[\mathbb{E}[X \mathbb{1}_A] = \mathbb{E}[Y \mathbb{1}_A].\]

Properties:

Uniqueness: If $Y$ and $Y’$ satisfy the above conditions, then $Y = Y’$ almost surely.
Tower Property: If $G \subset H \subset \mathcal{F}$,
\[\mathbb{E}[\mathbb{E}[X \mid H] \mid G] = \mathbb{E}[X \mid G].\]
Integrability: $\mathbb{E}[\lvert Y\rvert] < \infty$.
Independence: If $X$ is independent of $G$, then:
\[\mathbb{E}[X \mid G] = \mathbb{E}[X].\]

Filtrations and Adapted Processes

A stochastic process $X$ is defined as:

\[X := (X_n)_{n \geq 0}, \quad X_n \in m\mathcal{F} \quad (\forall n).\]

A filtration $(\mathcal{F}_n)_{n \geq 0}$ satisfies:

\[\mathcal{F}_0 \subset \mathcal{F}_1 \subset \mathcal{F}_2 \subset \cdots\]

which represents an increasing sequence of information sets over time.

Definition: Adapted Processes

A stochastic process $X$ is said to be $(\mathcal{F}_n)$-adapted if:

\[X_n \in m\mathcal{F}_n, \quad \forall n \geq 0.\]

Definition: Martingales, Supermartingales, and Submartingales

Let $X$ be an $(\mathcal{F}_n)$-**adapted **process, and $\mathbb{E}[\lvert X_n\rvert]<\infty$ for all $n$. Then:

$X$ is a supermartingale relative to $(\mathcal{F}_n, \mathbb{P})$ if:
\[\mathbb{E}[X_{n+1} \mid \mathcal{G}_n] \leq X_n, \quad \forall n \geq 0.\]
$X$ is a submartingale if $-X$ is a supermartingale:
\[\mathbb{E}[X_{n+1} \mid \mathcal{G}_n] \geq X_n, \quad \forall n \geq 0.\]
$X$ is a martingale if:
\[\mathbb{E}[X_{n+1} \mid \mathcal{G}_n] = X_n, \quad \forall n \geq 0.\]

Example: A Martingale Process

Let $(Y_n)_{n \geq 1}$ be an i.i.d. sequence on $(\Omega, \mathcal{F}, \mathbb{P})$. Define:

\[X_n = X_0 + \sum_{i=1}^{n} Y_i.\]

Suppose:

\[\mathbb{E}[Y_n] = 0, \quad \mathbb{E}[|X_0|] < \infty.\]

We also assume:

\[\mathcal{F}_0 = \sigma(X_0), \quad X_0 \perp\kern-5pt\perp (Y_i)_{i\geq1}.\]

Since:

\[\mathbb{E}[X_{n+1} \mid \mathcal{F}_n] = \mathbb{E}[X_n + Y_{n+1} \mid \mathcal{F}_n] = X_n + \mathbb{E}[Y_{n+1} \mid \mathcal{F}_n] = X_n,\]

it follows that $(X_n)_{n \geq 0}$ is a martingale.

Properties of Martingales

Proposition: If $X$ is a martingale, then for all $n \geq 0$ and $k \geq 0$:

\[\mathbb{E}[X_{n+k} \mid \mathcal{F}_n] = X_n.\]

Taking expectations:

\[\mathbb{E}[X_n] = \mathbb{E}[X_0], \quad \forall n \geq 0.\]

Martingales and Convex Functions

Proposition: If $X$ is a martingale and $\varphi$ is a convex function such that $\varphi(X_n)$ is integrable for all $n \geq 0$, then:

\[\varphi(X_n) \text{ is a submartingale}.\]

(Jensen’s Inequality applied to conditional expectations.)

Example: Filtration-Generated Martingale

If $\mathbb{E}[\lvert X\rvert] < \infty$, define:

\[X_n := \mathbb{E}[X \mid \mathcal{F}_n], \quad \forall n \geq 0.\]

Then $(X_n)_{n \geq 0}$ is a martingale.

Predictable Processes and Martingale Transforms

Let $(X_n)_{n \geq 0}$ be an adapted process and let $(C_n)_{n \geq 0}$ be another adapted process.

Define the martingale transform:

\[(C \cdot X)_n := \sum_{k=1}^{n} C_k (X_k - X_{k-1}).\]

If $C_k$ satisfies:

\[C_k \in m\mathcal{F}_{k-1}, \quad \forall k \geq 1,\]

then $(C_k)$ is called a predictable process.

Properties of Martingale Transforms

Theorem: Supermartingale Property of Martingale Transforms

Let $X$ be a supermartingale, and let $(C_n)_{n \geq 0}$ be a non-negative, bounded, and predictable process. Then the process $(C \cdot X)_n$ is also a supermartingale.

Special Cases:

If $X_n \in L^2(\Omega, \mathcal{F}, \mathbb{R})$ for all $n$, then boundedness can be replaced by $C_n \in L^2(\Omega, \mathcal{F}, \mathbb{P})$.
If $X$ is a martingale and $C$ is bounded and predictable, then $(C \cdot X)$ is also a martingale.

Proof (Case 1)

Since $(C_n)$ is predictable, we expand the conditional expectation:

\[\mathbb{E}[(C \cdot X)_{n+1} \mid \mathcal{F}_n] = (C \cdot X)_n + \mathbb{E}[C_{n+1} (X_{n+1} - X_n) \mid \mathcal{F}_n].\]

Using the supermartingale property of $X$:

\[\mathbb{E}[X_{n+1} \mid \mathcal{F}_n] \leq X_n,\]

we obtain:

\[\mathbb{E}[(C \cdot X)_{n+1} \mid \mathcal{F}_n] \leq (C \cdot X)_n.\]

Example: Simple Symmetric Random Walk

Consider a simple symmetric random walk $(S_n)_{n \geq 0}$ defined by:

\[S_0 = 0, \quad S_n = \sum_{i=1}^{n} Y_i,\]

where $Y_i$ are i.i.d. with:

\[\mathbb{P}(Y_i = 1) = \mathbb{P}(Y_i = -1) = \frac{1}{2}.\]

Define the stopping time:

\[T = \inf \{ n \geq 0 \mid S_n = 1 \}.\]

Then:

$\mathbb{P}(T < \infty) = 1$.
$\mathbb{E}[S_T] = 1 > 0 = \mathbb{E}[S_0]$.
$\mathbb{E}[T] = \infty$.

Remark: The following Doob’s Optional Stopping Theorem gives us some sufficient conditions when $\mathbb{E}[X_T] = \mathbb{E}[X_0]$ for a martingale $X$.

Stopping Times and Optional Stopping Theorem

Definition: Stopping Time

A random variable $T: \Omega \to {0,1,2,\dots} \cup {\infty}$ is a stopping time with respect to the filtration $(\mathcal{F}_n)$ if:

\[\{T \leq n\} = \{ \omega \mid T(\omega) \leq n \} \in \mathcal{F}_n, \quad \forall n \geq 0.\]

Remark: It is equivalent to $T$ is a stopping time iff ${T=n}\in \mathcal{F}_n$ for all $n\geq0$, i.e. the decision to stop at time $T$ must be measurable w.r.t the information known at that time.

Example: Hitting Time

Let $(X_n)_{n \geq 0}$ be an adapted process and let $B$ be a Borel subset of $\mathbb{R}$. Define:

\[T = \inf \{ n \geq 0 \mid X_n \in B \}.\]

(With the convention $\inf \varnothing = \infty$.)

Since:

\[\{T \leq n\} = \bigcup_{k=0}^{n} \{X_k \in B\} \in \mathcal{F}_n,\]

it follows that $T$ is a stopping time.

Stopped Process and Supermartingales

Let $X$ be a supermartingale and let $T$ be a stopping time. Define the stopped process:

\[Y_n = X_{T\wedge n} = X_n \mathbb{1}_{\{n \leq T\}} + X_T \mathbb{1}_{\{n > T\}}.\]

Theorem: Stopped Supermartingale

If $X$ is a supermartingale and $T$ is a stopping time, then the stopped process $(Y_n)_{n \geq 0}$ is also a supermartingale.

Proof:

Define the predictable process:

\[C_n = \mathbb{1}_{\{n \leq T\}}.\]

Then:

\[Y_n = X_0 + (C \cdot X)_n.\]

Further, since

\[\{C_n=0\}=\{T<n\}=\{T\leq n-1\}\in m\mathcal{F}_{n-1},\quad \{C_n=1\}=\{C_n=0\}^{c}\in m\mathcal{F}_{n-1},\]

$C_n$ is predictable, we conclude that $(Y_n)$ is a supermartingale.

Theorem: Doob’s Optional Stopping Theorem

Let $T$ be a stopping time and let $X$ be a supermartingale. Then:

\[\mathbb{E}[X_T] \leq \mathbb{E}[X_0].\]

This holds if any of the following conditions are met:

$T$ is bounded.
$X$ is bounded and $T$ is finite.
$\mathbb{E}[T] < \infty$ and there exists a constant $K$ such that:
\[|X_n - X_{n-1}| \leq K, \quad \forall n \geq 0.\]

Proof: Case 3

We use the fact that for any stopping time $T$:

\[X_{T \wedge n} - X_0 = \sum_{i=1}^{T \wedge n} (X_i - X_{i-1}).\]

Taking expectations:

\[\mathbb{E}[X_{T \wedge n}] \leq \mathbb{E}[X_0].\]

Further,

\[|X_{T \wedge n}|\leq \left|\sum_{i=1}^{T \wedge n} (X_i - X_{i-1})\right|+|X_0|\leq \sum_{i=1}^{T \wedge n}|X_i - X_{i-1}|+|X_0|<TK+|X_0|.\]

Using the Dominated Convergence Theorem (DCT), we obtain: $\mathbb{E}[X_T] \leq \mathbb{E}[X_0].$

Exercises

Let $X$ be a supermartingale and $T$ be a stopping time satisfying one of the conditions in Doob’s theorem. Show that:

\[\mathbb{E}[X_T \mathbb{1}_{\{T>n\}} \mid \mathcal{F}_n] \leq X_n \mathbb{1}_{\{T >n\}}.\]

For a stopping time $T$, define:

\[\mathcal{F}_T := \{ A \in \mathcal{F} \mid A \cap \{T \leq n\} \in \mathcal{F}_n, \quad \forall n \geq 0 \}.\]

Theorem: Doob’s Optional Sampling Theorem

Suppose $T$ and $S$ are bounded stopping times with $S \leq T$, and $X$ is a martingale. Then:

\[\mathbb{E}[X_T \mid \mathcal{F}_S] = X_S.\]

Proof:

Let $A \in \mathcal{F}_S$. Then:

\[\mathbb{E}[X_T \mathbb{1}_A] = \sum_{n=0}^{N} \mathbb{E}[X_T \mathbb{1}_{\{T=n\}}].\]

Now, let $X$ be an adapted integrable process. Assume $X_0 = 0$. Then $X$ is a martingale if and only if:

\[\mathbb{E}[X_T] = 0, \quad \text{for all bounded stopping times } T.\]

Proof:

From the martingale property:

\[\mathbb{E}[X_{n+1} \mid \mathcal{F}_n] = X_n, \quad \forall n \geq 0.\]

Applying this iteratively, we obtain:

\[\mathbb{E}[X_{n+1} \mathbb{1}_A] = \mathbb{E}[X_n \mathbb{1}_A], \quad \forall A \in \mathcal{F}_n.\]

For a stopping time $T(\omega)$, define:

\[T(\omega) = \begin{cases} n, & \omega \in A, \\ n+1, & \omega \notin A. \end{cases}\]

Then:

\[\mathbb{E}[X_T] = \mathbb{E}[X_n \mathbb{1}_A + X_{n+1} \mathbb{1}_{A^c}].\]

Rearranging,

\[\mathbb{E}[X_n \mathbb{1}_A] = -\mathbb{E}[X_{n+1} \mathbb{1}_{A^c}] = -(\mathbb{E}(X_{n+1})-\mathbb{E}(X_{n+1}\mathbb{1}_{A}))=\mathbb{E}(X_{n+1}\mathbb{1}_{A}).\]

Convergence of Supermartingales

Let $X$ be a supermartingale. Consider:

\[\lim_{n \to \infty} X_n = ?\]

Example: Symmetric Random Walk

Let $(S_n)_{n \geq 0}$ be a simple symmetric random walk with $S_0 = 0$. In this case:

\[\lim_{n \to \infty} S_n(\omega) \text{ does not exist (a.s.).}\]

Definition: $L^1$-Bounded Processes

A process $X$ is bounded in $L^1$ if:

\[\sup_n \mathbb{E}[|X_n|] < \infty.\]

Proposition: Supermartingale Convergence

If $X \geq 0$ and $X$ is a supermartingale, then:

\[\mathbb{E}[|X_n|] = \mathbb{E}[X_n] \leq \mathbb{E}[X_0] < \infty.\]

Doob’s Upcrossing Inequality

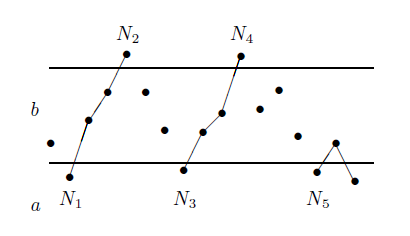
If $a < b$, define the number of upcrossings:

\[U_N([a, b]) = \# \text{ of upcrossings on } [0, N].\]

Define:

\[C_1 = \mathbb{1}_{\{X_0 < a\}}, \quad C_n = \mathbb{1}_{\{C_{n-1} = 1\}} \mathbb{1}_{\{X_{n-1} \leq b\}} + \mathbb{1}_{\{C_{n-1} = 0\}} \mathbb{1}_{\{X_{n-1} < a\}}.\]

Then:

\[Y_N = (C \cdot X)_N \geq (b-a) U_N([a, b]) - (X_N - a)^-.\]

Since $X$ is a supermartingale, we have:

\[\mathbb{E}[Y_N] \leq 0.\]

Thus,

\[(b-a) \mathbb{E}[U_N([a, b])] \leq \mathbb{E}[(X_N - a)^-].\]

Taking limits:

\[(b-a) \mathbb{E}[U_{\infty}([a, b])] \leq \sup_N \mathbb{E}[|X_N|] + |a|.\]

Consequence:

\[\mathbb{P}(U_{\infty}([a, b]) < \infty) = 1 \quad \text{(a.s.)}.\]

Theorem: Supermartingale Convergence

Suppose $X$ is a supermartingale and is $L^\infty$-bounded. Then:

\[X_{\infty} := \lim_{n \to \infty} X_n \text{ exists a.s., and }\] \[\mathbb{E}[|X_{\infty}|] < \infty.\]

Proof:

Define the fluctuation set:

\[\begin{align*} \Lambda &:= \{ \omega \mid X_n(\omega) \text{ does not have a limit including }\infty \}\\ &=\{ \omega \mid \liminf X_n(\omega) < \limsup X_n(w)\}\\ &=\bigcup_{a,b\in\mathbb{Q},\ a<b}\{ \omega \mid \liminf X_n(\omega) < a < b < \limsup X_n(w)\}, \end{align*}\]

where let $\Lambda_{a,b}:={ \omega \mid \lim\inf X_n(\omega) < a < b < \lim\sup X_n(w)}$. Therefore, $\Lambda_{a,b}\subset {U_N([a, b])=\infty}$.

Hence,

\[\mathbb{P}(\Lambda_{a,b}) = 0\implies \mathbb{P}(\Lambda)=0.\]

Since $X_n$ is $L^1$-bounded, we have:

\[\sup_n \mathbb{E}[|X_n|] < \infty.\]

By Fatou’s Lemma:

\[\mathbb{E}[|X_{\infty}|] = \mathbb{E}[\lim|X_n|] \leq \liminf_{n \to \infty} \mathbb{E}[|X_n|] \leq \sup_n \mathbb{E}[|X_n|] < \infty.\]

Thus, $X_{\infty}$ is integrable.

Another question arises:

\[\mathbb{E}[X_{\infty} \mid \mathcal{F}_n] = \mathbb{E}[\lim_{m \to \infty} X_m \mid \mathcal{F}_n]\leq(?) \lim_{m \to \infty} \mathbb{E}[X_m \mid \mathcal{F}_n] \leq \lim X_n.\]

Consider the following example.

Example: Gambler’s Ruin Problem

Consider a random walk:

\[S_0 = 1, \quad S_n = 1 + \sum_{i=1}^{n} Y_i,\]

where:

\[\mathbb{P}(Y_i = 1) = p, \quad \mathbb{P}(Y_i = -1) = 1 - p.\]

Define:

\[T = \inf \{ n \mid S_n = 0 \}.\]

Define:

\[M_n = S_{n \wedge T}.\]

If $p \leq \frac{1}{2}$, then $M_n$ is a supermartingale, and:

\[M_{\infty} = 0.\]

If $p > \frac{1}{2}$, then:

\[\mathbb{P}(T = \infty) > 0.\]